billard-fdg

Billardtips: 2
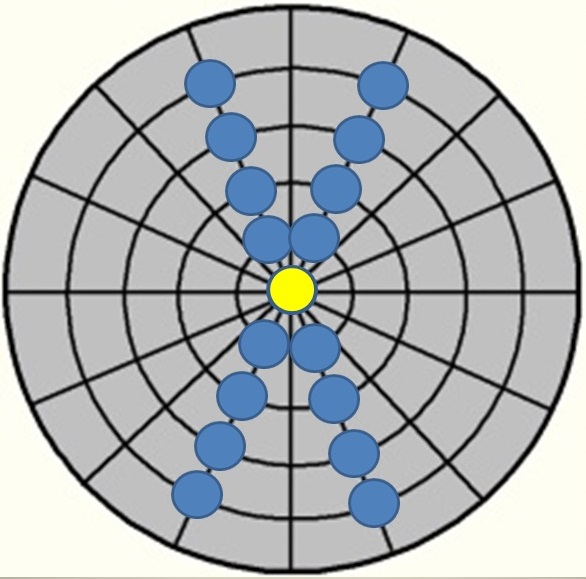
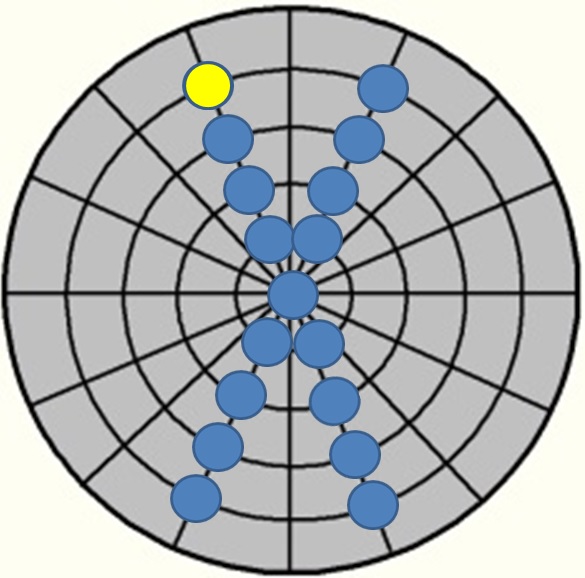
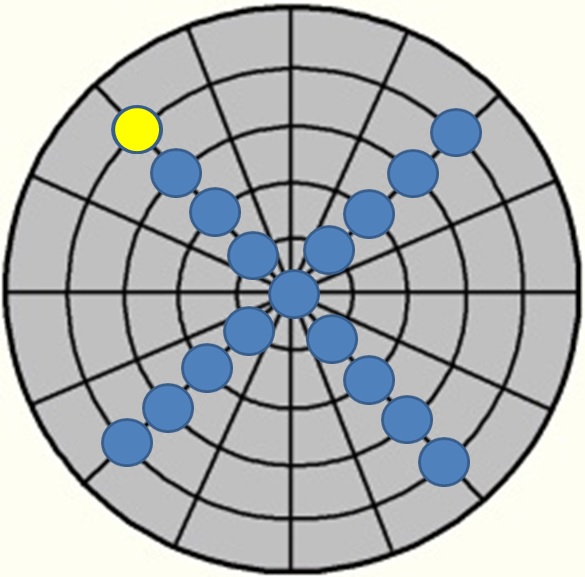
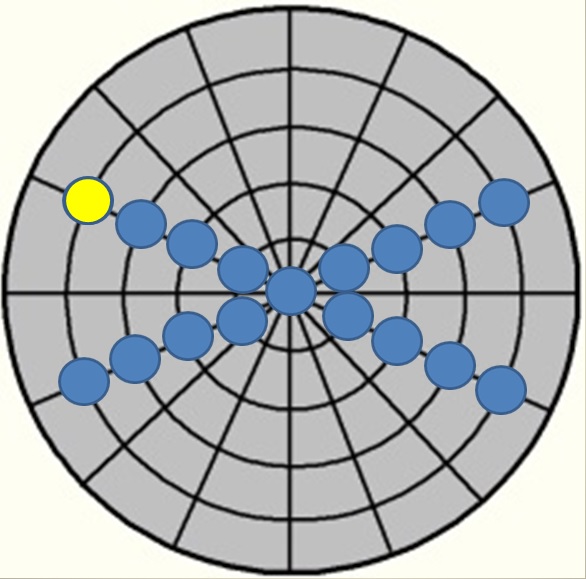
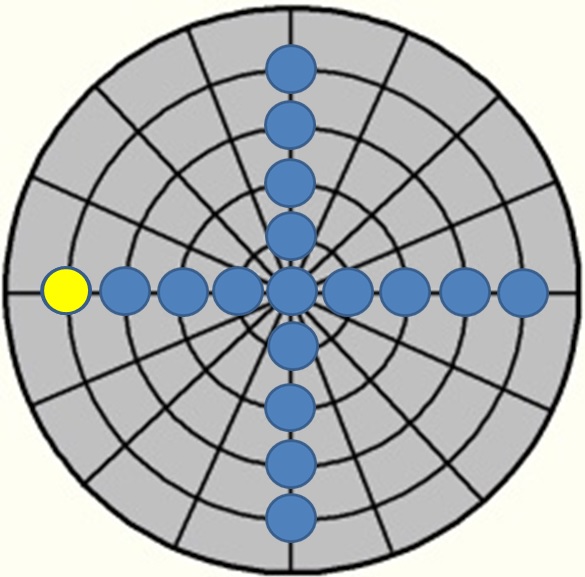
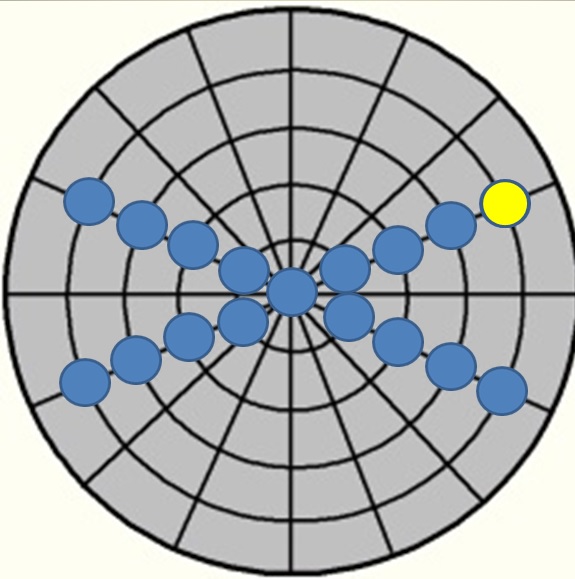
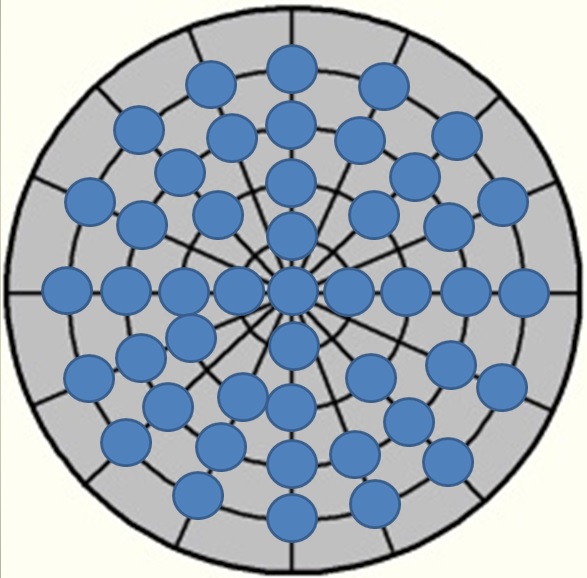
Der mathematische Stoßpunkt an Ball 1
Da jeder Stoßpunkt an Ball 1 einem mathematischen Wert entspricht ist es sinnvoll diese mathematischen Werte
zu kennen. Dies ist besondern im Einsatz von mathematischen Lösungssystemen Tuzul
im Dreiband von hohem Vorteil.
Das Wissen um die Bedeutung dieser mathematischen Werte darf nicht unterschätzt werden.
Grundvoraussetzung ist hier natürlich ein immer gleichbleibender Stoß/Stoßpunkt!

Man unterscheidet grundsätzlich in 2 Arten von Stoßpunktsystemen:
- dem offenen System
- dem numerischen System

Das numerische System:
Die Stoßpunkte im numerischen System sind immer ein TW der einem mathematischen Wert entspricht.
Dieser TW kann wie im Diamondsystem zwischen 0 und 20 liegen und ist nicht mathematisch berechenbar.
Er ist abhängig von der Startbande/Zielbande und dem Startpunkt.

Im Diamondsystem:
Im Diamonsystem wird als Grundregel mit einem Stoßpunkt agiert der oberhalb von Startpunkt 50 bei 15/20 liegt.
Lautet die Startbande B oder D kann der Stoßpunkt bis 0 wandern.
Dazu kommt noch das der Winkel von Ball 1 auf Ball 2 den Stoßpunkt um so mehr verkleinert je rechtwinkliger
der Winkel von Ball 1 auf Ball 2 ist.

Im Tuzul System:
Hier ist der TW immer eine feste mathematische Größe die in einer mathematischen Formel zur Anwendung kommt.
Dieser TW kann dann zwischen 0 und 30 liegen.
Standardwerte sind: 5, 10 , 15 , 20 , 25 , 30

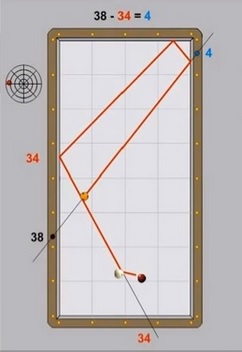
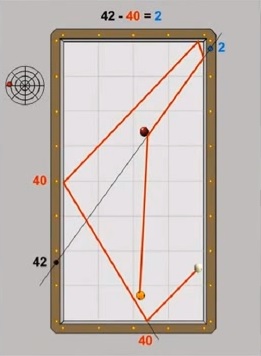
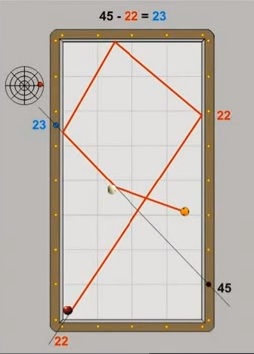
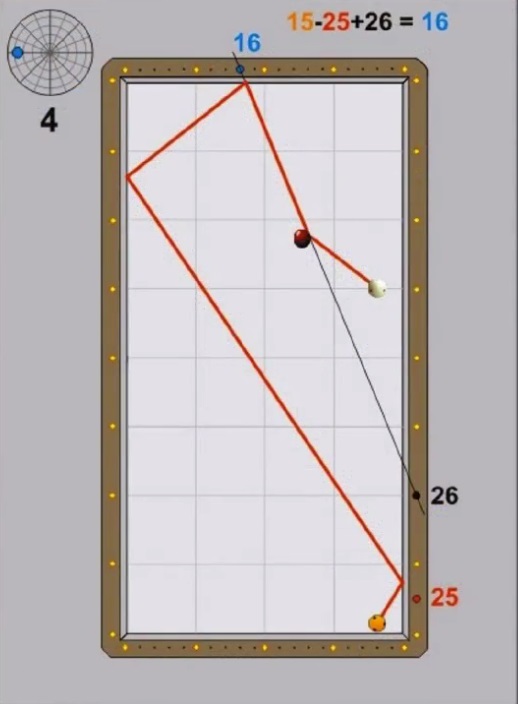
Die mathematische Lösungsformel lautet:
Z = (TW - ANK) + START

Die Skalierung der Banden kann je nach mathematischem Lösungssystem sehr unterschiedlich sein.

Das Fazit:
Während es im Dioamndsystem keine festen TW gibt kann dieser TW in Tuzul Lösungsystemen
variabel sein und ist immer ein mathematischer Wert der in der
mathematischen Lösungsformel verwendet wird.
Es gibt aber auch Tuzul Systeme in denen mit offenen Stoßpunkten agiert wird., also
aufbauend auf der jeweiligen Skalierung.